Revealed: The SARS-CoV-2 Sequencing Sham

The Paper Stefan Lanka Hoped Would Change The World

In late 2020, with the world now entirely locked down and the threat of forced or nearly-forced injections rising daily, the extraordinary Dr. Stefan Lanka, a former virologist, emailed out a short paper by a mathematician in Hamburg with astounding consequences.

Dr. Lanka and his colleagues’ many decades of work exposing the foundational problems with virology were now being echoed and built upon by a small group of doctors, scientists, journalists and thinkers in a quickly growing manner in 2020, and his revelations were beginning to reach the public in a significant way.

Yet a refrain was growing among the apologists for virology against many of Lanka’s claims. The refrain was simple - that perhaps he was correct about the pseudoscience of the earlier period of virology - but that recent virology was much more advanced and was based on the mathematical complexity of genomics - a complexity that critics simply couldn’t comprehend. 

Desperate to show this canard for what it was - that the so-called genetic sequencing of the SARS-CoV-2 “virus” was an illusion at best and a fraud at worst — Dr Lanka had approached an eminent mathematician to blow the smoke away from this mathematical complexity hiding the fraudulence behind the claims that a SARS-CoV-2 “virus” had ever been found at all.

The paper was sent out to a handful of Lanka’s friends, myself included, but with Substack still in its infancy and most covid-critical doctors and scientists still without even a website, somehow the paper was never published on the internet. 

Below is a reprint of the entire paper, published here in English, I believe, for the first time. Hopefully it can garner some attention from mathematics professors, geneticists, and lay people alike.

The mathematician Lanka turned to, calling himself only “A Mathematician From Hamburg” to avoid reprisals against his career, examined the central academic paper authored by the now infamous Dr. Fan Wu et al in Wuhan, China and printed in the February 2020 issue of the journal Nature: “A new coronavirus associated with human respiratory disease in China” which claimed to have genetically sequenced a “novel virus” later named SARS-CoV-2.

The mathematician in Hamburg downloaded the full data set and the appropriate software Fan Wu had used to claim the discovery of SARS-CoV-2, and then repeated Wu’s procedures. He returned to Dr. Lanka a clear refutation of the basic reasoning used to conclude that a novel virus had ever been discovered at all.

To understand this stunning work, one must understand the basic tenets of how Fan Wu and his colleagues ever claimed to have sequenced a virus in the first place. What they did is not a-traditional in the field of virology, but once understood, it beggars the imagination how such a sequence of steps could ever have been accepted as the central basis upon which to claim anything at all, let alone a scientific field, let alone the terrorizing and shutting down of the entire world. 

Some background: By the 1980s, virology still had yet to find and isolate a single virus (it still hasn’t), and had changed little since its seminal claims in the 1950’s that placing snot mixed with antibiotics on monkey kidney cells proved the existence of a virus in the snot if the kidney cells deteriorated - ignoring the many other reasons such deterioration might take place. The second, and frankly, only other significant process done in virology at the time was taking photographs of obliterated snot under an electron-micrograph. If “virologists” saw circles (or another predetermined shape) in the imagery, they claimed this was further proof that a “virus” had been found - again ignoring the problem that they had no reason to conclude that their theoretical “viruses” were the only possible reason one might see a circle or another predetermined shape. 

The obvious inconclusiveness and gaping logical flaws of these “experiments” was perhaps beginning to wear thin and the field had made few advancements upon the imagination of the public sphere. 

When the computer revolution emerged simultaneously with the study of genomics, virology cast about for a way to study its theorized (yet still never found, isolated or proven to exist) particles using the new technology.

It’s worth noting that this was an entirely different process than what was used more generally in genomics. In other fields of genomics, one began with an actual isolated sample of the material in question (e.g a HORSE, a FLY, or a strain of BACTERIA, etc.) and catalogued what RNA could be found consistently in the isolated sample of such material. However, in virology, as they never had an actual sample of a  “virus” in question, isolated from the rest of human fluid, all they could do was catalogue the entirety of the genetic material in their snot samples, and then take guesses as to what their imagined virus might be made from.

Over the last forty years, this so-called “genetic sequencing” has become the central process by which people in lab coats (I cannot bring myself to call them scientists) claim to have since discovered new “viruses.” Essentially, the steps are the following:

1. Find a person who is sick, ASSUME they are sick due to a virus, and then take a sample of their snot or “lung fluid.”

2. Combine this fluid with salt water and antibiotics (and often many other ingredients).

3. Feed this fluid mixture into a machine which physically breaks apart the material into tens of millions of genetic fragments.

4. Submit this mixture to a PCR process to amplify the number of the RNA fragments, including the “amplification” of any specific RNA fragments the virologists expect to find. 

5. Have this machine-computer create a list of these genetic fragments.

6. Have the computer exclude a (not-at-all conclusive) partial list of known human endogenous fragments from its data-set.

7. Have the computer employ probability algorithms to find fragment sequences that overlap and create possible "contigs" - then pick out the longest sequences amongst these that can be theoretically stitched together by the computer.

8. Have the computer output a list of these combinations which are most similar to sequences that were also hypothetically created and attributed to imagined 'viruses' in the past." 

9. The virologists then pick amongst these combinations, deciding by consensus, the one computer-theorized sequence they think is the virus making the patient sick. If they cannot  even come close to matching one of the sequences the computer assembled to a previously theorized sequence, then the virologists claim what they have found must be a “novel virus” and pick by consensus from among the listed combinations outputted by the computer the one they best guess is the virus (and not just meaningless acidic jargon).

For those who want a deeper dive into this nonsense, I cover this in depth in the documentary The Viral Delusion at www.theviraldelusion.com, Mike Stone covers it in great detail on his blog viroliegy.com, Dr. Mark Bailey tears it apart in his paper “A Farewell To Virology” and Dr. Tom Cowan , Dr. Andy Kaufman and Amandha Volmer (among others) have countless hours detailing the absurdities of this in their videos. You can of course also read the original Fan Wu paper to see their outline of these steps.  But as the below paper makes clear, even the many doctors and scientists I spoke with in The Viral Delusion underestimated the mathematical nonsense that was employed in the Fan Wu paper (but buried deep in the methodology section)- nonsense which our esteemed mathematician reveals below.  

Of course I can already hear you shouting - stop, wait! We don’t need to go any further. This is already a series of steps that is ludicrously lacking in methodological soundness. Yes, I know. To make the point for new readers more bluntly, one could use this same series of steps to clam the discovery of any novel genetic sequence whatsoever - whether it be a “virus” or “the devil’s mark,” “cooties” or proof of discovering the lingering genes of an alien. It’s a textbook example of pseudo-science built upon the logical sleight of hand known as “begging the question.” And that’s just the tip of the iceberg for logical problems with making any sort of conclusion based on the above steps. 

But let’s continue - for the refrain consistently from virology’s apologists was that none of these logical problems mattered, the math was so complex and so profound that it proved virology had been right all along, and anyone who questioned it simply couldn’t understand.

Enter the mathematician from Hamburg.  His paper is below, and you are welcome to skip to it of course. But it’s written in rather heady language, so I will take a moment to summarize it here.

As you will see, the mathematician began his analysis by downloading the data set of the complete RNA fragmentation from the original experiment and attempting to simply repeat the computer steps taken in the paper. 

He found that even these steps were not replicable by a computer.   The sequences output by the software which claimed to find “SARS-CoV-2” could not be output by another computer running the same software. 

This is no small point! As most know, basic scientific rigor demands that experiments must be replicable for their conclusions to be considered valid - but the non-replicable nature of the SARS-CoV-2 sequencing goes far beyond that.  We’re not talking about being able to replicate an experiment that happened in living nature; we are talking about a computer running the same software upon the same data-set not being able to replicate what was claimed to have happened on another computer running the same software on the same data-set! 

To make this clear, it’s as if Fan Wu et al claimed their computer could spell a word from a Scrabble set with more “P”s than the Scrabble set included. 

However, that is only the beginning. The mathematician went ahead and assumed that the original data set and original output were correct to continue his analysis. 

What he found lays bare that any conclusion based on this data that the patient studied in Wuhan had a novel virus was entirely unsubstantiated.  

First, again, he makes clear that the sequences Fan Wu et al claimed to have outputted could NOT be assembled from the bits of RNA catalogued by the computer in the patient sample. 

Second, he found that there was no way to tell whether the assembled sequence (later called SARS-CoV-2) came from human or non-human RNA. In other words, there is nothing in the experiment to show whether the sequence was assembled FROM a “virus” in the sample or just from random bits of RNA in the sample.

Third, he found that there was no way to tell whether the assembled sequence came from actually-existing RNA in the sample or was compiled from RNA markers that were there simply as a by-product of the PCR amplification the sample was exposed to. 

Fourth, he found that up to 17% of the final sequence was based on RNA contigs specifically targeted and then “found” by the PCR process at cycle thresholds of ct 35 to 45, cycle counts well known in the literature to “find” anything you want. 

Fifth, he found that these contigs were significantly MORE likely to have come from the PCR process itself than the original sample, and that it was HIGHLY unlikely that all of the SARS-CoV-2 sequence contigs (or even most) came from the original sample.

Sixth, he found that contigs in the remaining data sample AFTER the Fan Wu paper claims to have filtered it for known human RNA, matched known human RNA. 

Seventh, he found that the final (SARS-CoV-2) sequence claimed to match “corona viruses” didn’t even match these theoretical sequences unless an “error rate” was included that was over 10 percent.

Eighth, he sought to discover whether one could take the sample and “find” other claimed viruses in it. He searched for “Hepatitus” and “HIV” and found BOTH of them to have lower error rates than “SARS-CoV-2.”

Ninth, he searched for the claimed sequences of “Ebola”  and “Marburg virus” and “found” these in the sample as well, at comparable error rates to “SARS-CoV-2.”

Tenth, he found that no control experiments were conducted to rule out any of the above or other possibilities. 

In conclusion, the mathematician writes “we were able to substantiate our hypothesis that the claimed viral genome sequences are misinterpretations in the sense that they have been or are being constructed unnoticed from non-viral nucleic acid fragments.”

In other words there is nothing in the math to suggest concluding that a novel virus had been found, or was in any way the cause of the original man’s sickness - in fact it is the reverse - it is MORE likely based on the data that the sequence compiled by the computer and that Fan Wu claimed to be “SARS-CoV-2” was not from a “virus.”

A close read of the mathematician’s paper indeed suggests and explains that it’s far MORE likely that the “SARS-CoV-2” sequence was built from random bits of RNA floating in the sample combined with specifically-generated “discoveries” of RNA fragments created by PCR for the very purpose of “finding” them.  

When we remember that this Fan Wu paper formed, in essence, the bedrock of the “scientific” foundation of the claimed pandemic, it’s hard to say whether one should laugh or cry. It was upon the conclusion of this paper that the PCR testing was designed, and the world was tested for this “novel virus.” It was upon this paper that synthetic “virus” sequences were built by laboratories to test the “virus” for its qualities and to study its “nature.”

It was upon this claimed sequence by Fan Wu et al that media pundits and pseudo-scientist apologists claimed mathematical complexity beyond the ability of anyone outside of their field to understand or comment upon, and thus sought to shut down any and all criticism. 

And it was upon this paper’s conclusions that the claimed “vaccine” was said to have been designed, and billions of people pressured into injecting themselves. It was the logical and mathematical ruse at the very heart of the pandemic.

But lest I steal the thunder from his analysis further, here is the reprint of the mathematician’s paper below. 

Do share your thoughts after reading (and a big thank you to Petra Liverani for the proper formatting of the paper on Substack!)

Structural analysis of sequence data in virology

An elementary approach using SARS-CoV-2 as an example

Author

By a mathematician from Hamburg, who would like to remain unknown

Abstract

De novo meta-transcriptomic sequencing or whole genome sequencing are accepted methods in virology for the detection of claimed pathogenic viruses. In this process, no virus particles (virions) are detected and in the sense of the word isolation, isolated and biochemically characterized. In the case of SARS-CoV-2, total RNA is often extracted from patient samples (e.g.: bronchoalveolar lavage fluid (BALF) or throat- nose swabs) and sequenced. Notably, there is no evidence that the RNA fragments used to calculate viral genome sequences are of viral origin.

We therefore examined the publication "A new coronavirus associated with human respiratory disease in China" [1] and the associated published sequence data with bioproject ID PRJNA603194 dated 27/01/2020 for the original gene sequence proposal for SARS-CoV-2 (GenBank: MN908947.3). A repeat of the de novo assembly with Megahit (v.1.2.9) showed that the published results could not be reproduced. We may have detected (ribosomal) ribonucleic acids of human origin, contrary to what was reported in [1]. Further analysis provided evidence for possible nonspecific amplification of reads during PCR confirmation and determination of genomic termini not associated with SARS-CoV-2 (MN908947.3).

Finally, we performed some reference-based assemblies with additional genome sequences such as SARS-CoV, Human immunodeficiency virus, Hepatitis delta virus, Measles virus, Zika virus, Ebola virus, or Marburg virus to study the structural similarity of the present sequence data with the respective sequences. We have obtained preliminary hints that some of the viral genome sequences we have studied in the present work may be obtained from the RNA of unsuspected human samples.

Keywords

SARS-CoV-2, COVID-19, Virus, De novo Assembly, Whole genome sequencing, WGS, Bioinformatics, PCR, SARS-CoV, Bat SARS-CoV, Human immunodeficiency virus, HIV, Hepatitis virus, Measles virus, Zika virus, Ebola virus, Marburg virus.

Introduction

To construct viral genome sequences, nucleic acids (RNA or DNA) are isolated from various nucleic acid sources such as bronchoalveolar lavage fluid (BALF) [1, 2], nasopharyngeal swabs [3, 4, 5, 6, 12, 13], cell culture components or cell culture supernatants [2, 11, 12, 13, 14, 16], as well as from human [8, 9, 10, 16] and animal samples [7, 15] and sequenced. In this process, the nucleic acids obtained are not exclusively from previously isolated (virus) particles, i.e., separated from everything else, but often from the entire sample. Thus, the origin of the nucleic acid fragments used to calculate the genome sequences is a priori unclear.

In the case of ribonucleic acids (RNA), this is first transcribed into cDNA using RNA- dependent DNA polymerase. The DNA or cDNA is then fragmented with the aid of enzymes and amplified by polymerase chain reaction (PCR) before the actual sequencing, i.e., the determination of the nucleotide sequence of the short DNA or cDNA fragments, takes place. During amplification, in addition to random primer sequences (random hexamers), highly specific primer sequences are also used depending on the reference or target genomes under consideration [e.g.: 1, 3, 4, 5, 6, 7, 8, 17, 18]. Finally, the sequence data thus obtained are processed using bioinformatics algorithms.

Two common methods for determining viral genome sequences represent de novo meta-transcriptomic assembly [1, 12] and whole genome sequencing [3, 4, 5, 6, 17, 18]. While de novo meta-transcriptomic assembly often uses no reference sequences or only downstream reference sequences, whole genome sequencing uses a large number of specific primer sequences, some of which already together cover 4% to 17% of the target genome [1, 17]. For amplification of the cDNA, 35 to 45 cycles are often used [1, 6, 17]. 

In the case of SARS-CoV-2 (GenBank: MN908947.3) [1], the viral genome sequence proposal was calculated by de novo meta-transcriptomic assembly of total RNA from the BALF of a patient in Wuhan, China. The assemblers Megahit (v.1.1.3) and Trinity (v.2.5.1) were used to assemble the contigs. Megahit generated a total of 384,096 (200 nt - 30,474 nt) and Trinity computed 1,329,960 (201 nt - 11,760 nt) contigs. The large differences between the two assemblages are noteworthy. According to [1], the longest contig assembled with Megahit showed a high nucleotide similarity (89.1%) with the genome bat SL-CoVZC45 (GenBank: MG772933) and was used to design primers for PCR confirmation and genome termini.

Viral genome organization was determined by sequence alignment to two representative species of the genus Betacoronavirus, a human-associated coronavirus (SARS-CoV Tor 2, GenBank: AY274119) and a bat-associated coronavirus (bat SL- CoVZC45, GenBank: MG772933).

No pathogenic viral particle uniquely associated with the MN908947.3 sequence was identified and biochemically characterized from the patient sample. Rather, total RNA was extracted and processed from a patient's BALF. Evidence is lacking that only viral nucleic acids were used to construct the claimed viral genome for SARS-CoV-2. Further, with respect to the construction of the claimed viral genome strand, no results of possible control experiments have been published. This is equally true for all other reference sequences considered in the present work. In the case of SARS-CoV-2, an obvious control would be that the claimed viral genome cannot be assembled from unsuspected RNA sources of human, or even other, origin.

In the present publication, we investigated the reproducibility of de novo assemblies using the original published sequence data for the original work on coronavirus SARS- CoV-2 [1]. We further investigated the structural similarity of the present sequence data with other publicly available viral reference sequences for (bat) SARS-CoV [1, 7, 13, 14], Human immunodeficiency virus [8], Hepatitis delta virus [9], Measles virus [11, 12], Zika virus [10], Ebola virus [15] and Marburg virus [16] (Tables and Figures: Table 3). For this purpose, we present here a simple bioinformatics protocol. To validate our results, we also considered randomly generated and fictional genome sequences to rule out pure randomness in our results.

Main section

Renewed de novo assembly of published sequence data

To repeat the de novo assembly, we downloaded the original sequence data (SRR10971381) from 27/01/2020 on 11/30/2021 using the SRA tools [19] from the Internet. To prepare the paired-end reads for the actual assembly step with Megahit (v.1.2.9) [20], we used the FASTQ preprocessor fastp (v.0.23.1) [21]. After filtering the paired-end reads, 26,108,482 of the original total of 56,565,928 reads remained, with a length of about 150 bp. A large proportion of the sequences, presumably a majority of those of human origin were overwritten by the authors with "N" for unknown and therefore filtered out by fastp. This is to be regarded as problematic in the sense of scientificity, since not all steps can be retraced or reproduced. For the elaborate contig generation from the remaining short sequence reads, we used Megahit (v.1.2.9) using the default setting.

We obtained 28,459 (200 nt - 29,802 nt) contigs, significantly less than described in [1]. Deviating from the representations in [1], the longest contig we assembled comprised only 29,802 nt, 672 nt less than the longest contig with 30,474 nt, which according to [1] comprised almost the entire viral genome. Our longest contig showed a perfect match with the MN908947.3 sequence at a length of 29,801 nt (Tables and Figures, Tables 1, 2). Thus, we could not reproduce the longest contig of 30,474 nt, which is so important for scientific verification. Consequently, the published sequence data cannot be the original reads used for assembly.

After assembling the contigs, we determined the respective coverage richness by mapping the short sequences to the 28,459 determined contigs using Bowtie2 (v.2.4.4) [22]. We then matched the 50 contigs with the highest coverage abundance and the 50 longest contigs to the nucleotide database (Blastn) on 12/05/2021 and 12/20/2021, respectively. The detailed query results can be found in Tables and Figures: Tables 1, 2.

A comparison of our results (Tables and Figures: Table 1) with those from [1, Supplementary Table 1. The top 50 abundant assembled contigs generated using the Megahit program.] show remarkable differences. In the following, the contig IDs from [1] are preceded by "1_" to better distinguish them from our contig IDs. In general, it can be stated that our query hits regarding the accession numbers do not exactly match those from [1]. With respect to the subject descriptions, we observed a good match for the most part. Further, with the exception of the longest contig (1_k141_275316), our contigs were found to have greater length and tended to have greater richness of coverage. The case is clear for contig 1_k141_179411 compared to contig k141_12253. The former has a length of 2,733 nt, while the latter is 5,414 nt long. This provides the first possible indication that nonspecific amplification of sequence reads not associated with SARS-CoV-2 occurred during PCR confirmation with primers constructed for MN908947.3 from 1_k141_275316 (30.474 nt).

At this point, the contig with the identification k141_27232, with which 1,407,705 sequences are associated, and thus about 5% of the remaining 26,108,482 sequences, should be discussed in detail. Alignment with the nucleotide database on 05/12/2021 showed a high match (98.85%) with "Homo sapiens RNA, 45S pre- ribosomal N4 (RNA45SN4), ribosomal RNA" (GenBank: NR_146117.1, dated 04/07/2020). This observation contradicts the claim in [1] that ribosomal RNA depletion was performed and human sequence reads were filtered using the human reference genome (human release 32, GRCh38.p13). Of particular note here is the fact that the sequence NR_146117.1 was not published until after the publication of the SRR10971381 sequence library considered here.

This observation emphasizes the difficulty of determining a priori the exact origin of the individual nucleic acid fragments used to construct claimed viral genome sequences.

Reference-based sequence structure analysis

Basically, we mapped the paired-end reads (2x151 bp) with BBMap [23] to the reference sequences we considered (Tables and Figures: Table 3) using relatively unspecific settings. We then varied the minimum length (M1) and minimum (nucleotide) identity (M2) with reformat.sh to obtain corresponding subsets of the previously mapped sequences with appropriate quality. Increasing minimum length M1 or minimum nucleotide identity M2 thereby increases the significance of the respective mapping. Subsequently, we formed consensus sequences with the respective subsets of selected quality with respect to the selected reference. We set all bases with a quality lower than 20 to "N" (unknown). A quality of 20 means an error rate of 1% per nucleotide, which can be considered sufficient in the context of our analyses. Finally, the assessment of the agreement between reference and consensus sequences was performed using BWA [24], Samtools [25], and Tablet [26]. The ordered pair (M1; M2) = (37; 0.6) was just chosen to give error rates F1 and F2, respectively, of less than 10% for reference LC312715.1. The results of all calculations performed are shown in Tables and Figures: Table 4.

The calculations show the highest significance for the choice of the ordered pair (37; 0.6), which can be seen from the highest error rates in each case. Comparable significance is provided by the ordered pairs (47; 0.50) and (25; 0.62). While the genome sequences associated with coronaviruses show error rates approximately above 10% for all ordered pairs considered (M1; M2), the error rates of the two sequences LC312715.1 (HIV) and NC_001653.2 (Hepatitis delta) are below 10% and decrease further for the ordered pairs (32; 0.60) and (30; 0.60). The sequence MG772933_short consists mainly of the part that is not coverable with the SARS-CoV-2 associated reads (see Tables and Figures: Figure 3). Again, no improvement could be achieved by reducing the values for M1 and M2. The error rates for sequences NC_039345.1 (Ebola virus), NC_024781.1 (Marburg virus), AF266291.1, and KJ410048.1 (Measles virus) are significantly higher than those for LC312715.1 and NC_001653.2. While the nucleic acid sequences used to calculate the former genomes were propagated in Vero cells, the nucleic acid sequences used for LC312715.1 and NC_001653.2 originated directly from samples of human origin (Tables and Figures: Table 3). Therefore, the question arises whether this result is due to structural differences of the respective nucleic acid sources or to the respective sequencing protocols used. For example, the reverse transcriptase used to convert RNA into cDNA or the primer sequences used for amplification as well as the amplification cycles could possibly lead to differences in the sequence libraries obtained.

The highest error rates F1 and F2 are shown by the randomly generated fictional genome sequences rnd_uniform, rnd_wuhan, rnd_wh_mk_1 and rnd_wh_mk_2, so the results found here are not purely random.

Graphical analysis of coverage distributions and read lengths

After observing the possibility of forming consensus sequences with high quality with respect to some reference sequences, we analyzed the coverage distribution of the associated short sequence reads (Tables and Figures: Figures 1-22) and the distribution of read lengths (Tables and Figures: Figures 23-25). To do this, we previously mapped the short sequence reads to their respective reference sequences using BBMap, ((M1; M2) = (37; 0.60)). In addition to the short sequences, we also mapped the 26 primer pairs [1, Supplementary Table 8. PCR primers used in this study.] for whole genome sequencing of SARS-CoV-2 (GenBank: MN908947.3) to the reference genomes under consideration. Subsequent analysis was performed via Tablet and the spreadsheet program Excel.

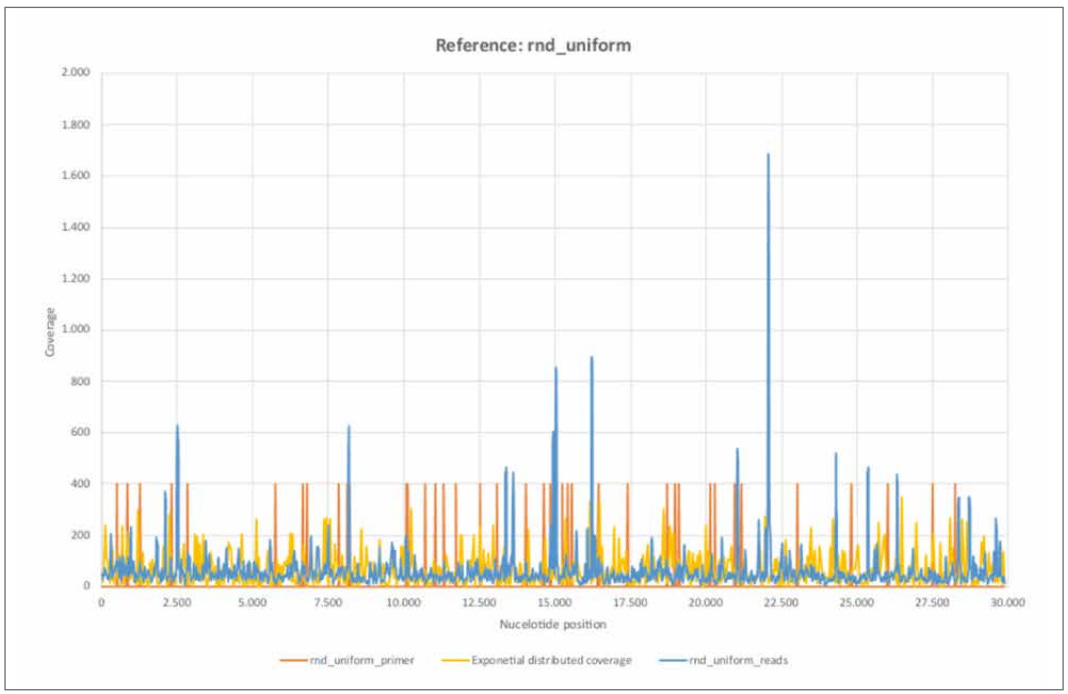
First, we consider the randomly generated reference rnd_uniform. Comparable observations hold for the randomly generated reference genomes rnd_wuhan, rnd_wh_mk_1, and rnd_wh_mk_2 (Tables and Figures: Figures 14-16).

Figure 13: Reference rnd_uniform.
a) rnd_uniform_reads mapped using BBMap, (M1; M2) = (37; 0,60).
b) rnd_uniform_primer mapped using BBMap.
c) Exponential distributed coverage was generated by stochastic simulation using the inversion method.
d) The 26 primer pairs ([1, Supplementary Table 8. PCR primers used in this study.]) are unevenly distributed across the entire reference genome. The primer positions correlate only weakly with areas of high nucleotide coverage, each comprising only a few nucleotides.
e) The distribution of rnd_uniform_reads appear largely random. The variance of the exponential distribution considered agrees well with the trimmed empirical variance.

The coverage (rnd_uniform_reads) varies randomly and relatively homogeneously across all nucleotide positions. The structure is comparable to the randomly generated coverage (exponential distributed coverage), although the variance appears somewhat lower. At a few isolated nucleotide positions, the coverage shows high coverage compared to the average, but each of these only spans a few contiguous nucleotide regions. A correlation with the primer positions is only weakly pronounced. The purely random appearing coverage with the short sequence reads correlates with a non- continuous mappable consensus sequence and high error rate F1 of 38.60%. Thus, the random (inner) nucleotide structure of the stochastically simulated reference sequence "rnd_uniform" is rather absent from the sequence data examined here.

In contrast, we now consider the reference genome for SARS-CoV-2 (GenBank: MN908947.3).

Figure 1: Reference MN908947.3.
a) MN908947.3_reads mapped with Bowtie2 under using default settings.
b) MN908947.3_primer mapped with BBMap.
c) Quantiles were determined from EN and VARN under the distribution hypothesis of a binomial distribution.
d) The 26 primer pairs ([1], Supplementary Table 8. PCR primers used in this study.) are evenly distributed across the entire reference genome. The primer positions correlate with areas of high nucleotide coverage.

In contrast to Figure 13, the coverage distribution shows more of a wave pattern with regular significantly increased nucleotide covers. The 26 primer pairs are evenly distributed over all nucleotide positions of the reference sequence. Primer positions are often located near nucleotide positions with high nucleotide coverage compared to the average. This indicates that not all parts of the reference genome were amplified equally. Assuming that all 29,903 nucleotide positions are equally likely to occur in SARS-CoV-2 associated reads, the coverage for each nucleotide position should be between the two lines with 99.5% probability (assuming a binomial distribution). This is not the case for approximately 90% of nucleotide positions. A priori, one would expect that if sufficient viral RNA is present in the sample and sufficient sequence pieces are read, homogeneous coverage of nucleotides within the viral genome would be achieved.

The following graph allows studying the distributions of the read lengths of the references just considered (rnd_uniform and MN908947.3)

Figure 23: a)-f)
Mapping with BBMap (M1, M2) = (37, 0.60).
Analysis in Excel.

 Figure 23e) shows the distribution of read lengths in the case of the reference "rnd_uniform". The average read length is 41.96 nt, only slightly to the right of the maximum of the distribution. In comparison, the distribution for reference MN908947.3, Figure 23a) shows a prominent (random) region similar to Figure 23e) and a distinct region with reads of about 150 nt in length. The average read length is over 110 nt. All reference sequences with a comparable and therefore rather random distribution of read lengths as in the stochastically simulated reference "rnd_uniform" (Tables and Figures: Figure 23d), f); Figure 24d), e), f); Figure 25a) - c)) also show high error rates F1 and F2 (Tables and Figures: Table 4).

This finding is underscored by the following analysis. In order to better understand the internal structure of the published approximately 56 million sequences, we considered the additional condition maxlength=100 for the sequence MN908947.3 during subset formation following mapping with BBMap in addition to M1 and M2.

Figure 2: Reference MN908947.3.
a) MN908947_reads mapped with Bowtie2 using default settings.
b) MN908947_short_reads mapped using BBMap, (M1; M2) = (37 (max. 100); 0.60).
c) Exponential distributed coverage was generated by stochastic simulation using the inversion method. The coverage distribution MN908947_short_reads show a more random pattern, but has a higher trimmed variance. This is mainly due to the few swings in the coverage distribution.

By excluding all mappable sequences longer than 100 nucleotides, essentially the approximately 120,000 reads associated with SARS-CoV-2 were removed. The coverage distribution of the remaining short sequences now appears random, analogous to Figure 13. Again, this correlates with high error rates R1 (29.90%) and R2 (29.96%). This indicates that no significant structure of reference MN908947.3 is included in the published sequences, except for the approximately 120,000 (Tables and Figures. Table 1) associated short reads.

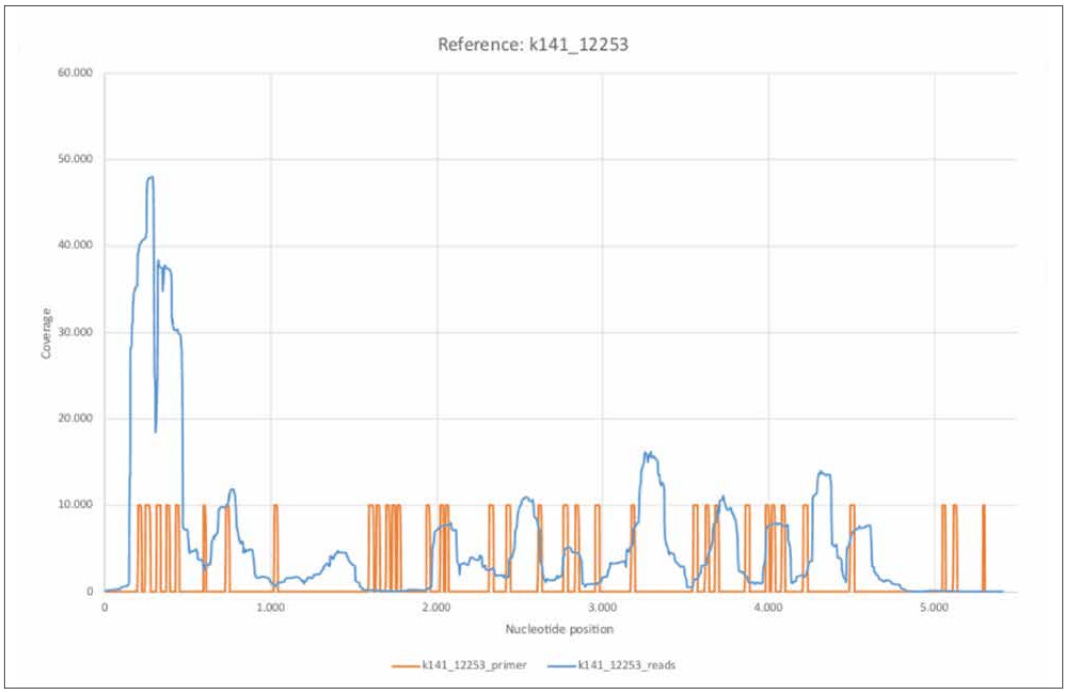
Before going into detail about some of the reference genomes we examined, we would first like to look at the coverage of two other contigs k141_12253 and k141_20796. While the contig identified as k141_12253 is characterized by a relatively high coverage, k141_20796 is among the three longest contigs calculated.

Figure 18: Reference k141_12253.
a) k141_12253_reads mapped with Bowtie2 using default settings.
b) k141_12253_primer mapped using BBMap.

The contig k141_12253 shows high similarity to the bacterium Leptotrichia (GenBank: CP012410.1). Of the 52 published primer sequences, 38 could be mapped to reference k141_12253 with a relatively high error rate of 37.30%. The coverage distribution turns out to be extremely inhomogeneous and shows, especially within the first 500 nucleotides, an extremely high nucleotide coverage compared to the average. The areas with a high coverage correlate with the determined primer positions. This could indicate that not exclusively SARS-CoV-2 associated reads were amplified in large amounts. Considering the relatively high error rate of 37.30%, this would imply a relatively non-specific amplification. Thus, the question arises whether reads obtained by amplifying the cDNA with the specific primer sequences were already present in the initial sample or were generated by the procedure itself.

Figure 21: Reference k141_20796.
a) k141_20796_reads mapped with Bowtie2 using default settings.
b) k141_20796_primer mapped using BBMap.

Contig k141_20796, which has a high match to the bacterium Veillonella parvula (GenBank: LR778174.1), shows lower coverage with associated reads compared to the contig with identification k141_12253. The nucleotide coverage structure is similar to that of SARS-CoV-2 (GenBank: MN908947.3). Notably, the coverage is again inhomogeneous, indicating uneven amplification. Due to the higher nucleotide length, 47 of the 52 published primer sequences could now be mapped to the reference contig with a mean error rate of 35.80%. Again, primer positions correlate well with areas of high nucleotide coverage. This could again indicate non-specific amplification of sequences not associated with SARS-CoV-2 (GenBank: MN908947.3).

In the present section, we will discuss in more detail the reference sequences "Human immunodeficiency virus 1" (GenBank: LC312715.1) and "Measles virus genotype D8 strain MVi/Muenchen" (GenBank: KJ410048.1). All other figures can be found in the supplementary materials (Tables and Figures: Figures 1-22 and Figures 23-25).

Figure 6: Reference LC312715.1.
a) LC312715.1_short_reads mapped using BBMap, (M1; M2) = (37; 0.60).
b) LC312715.1_primer mapped using BBMap.

Already in the previous section, a high structural similarity of the published sequences with the reference sequence LC312715.1 was shown. The calculated consensus sequence showed relatively lower error rates R1 = 8.60% and R2 = 8.83% compared to e.g. the SARS associated references. The Figure 6 shows clear differences to the Figure 13. The coverage distribution also shows more of a wave pattern with relatively regular areas of particularly high coverage and is therefore clearly different from the coverage distribution of the random reference "rnd_uniform". The distribution of read lengths (Figure 23b), compare also c)) also differs significantly from the more random distributions and shows a significant number of mappable reads with lengths up to about 110 nt. The average read length of 51.84 nt is also higher than for "rnd_uniform", for example.

Again, it is interesting to note the position of the primer sequences with respect to areas of high nucleotide coverage compared to medium coverage. A total of 46 of the 52 primer sequences could be assigned to the reference considered here with an error rate of 38.00%. Figure 6 suggests that short sequence reads associated with reference LC312715.1 were also amplified during PCR confirmation, despite the fact that the primer sequences could only be assigned to the reference with a relatively high error rate.

Finally, let us turn to reference KJ410048.1 (Measles virus).

Figure 10: Reference KJ410048.1.
a) KJ410048.1_short_reads mapped using BBMap, (M1; M2) = (37; 0,60).
b) KJ410048.1_primer mapped using BBMap.

The coverage distribution differs significantly from that in Figure 6 and shows some similarities with the distribution of associated sequence reads for "rnd_uniform", with less variation in areas of lower coverage. The distribution of read lengths (Tables and Figures: Figure 24d)) as well as the average read length of 42.38 are comparable to the data of "rnd_unifom" and also correlate with relatively high error rates F1=28.70% and F2=28.79%.

Discussion and outlook

We examined published sequence data (BioProject accession number PRJNA603194 in the NCBI Sequence Read Archive (SRA) database) on the genome sequence for SARS-CoV-2 (GenBank: MN908947.3) using a simple bioinformatics approach. The methods we used are not specific to SARS-CoV-2 and can be applied to other sequence data without special modifications.

First, we repeated the contig generation with Megahit (v.1.2.9) using the available sequence data and obtained significantly different results compared to the representations in [1]. In particular, we were unable to reproduce the longest contig with a length of 30,474 nt, which according to [1] comprised almost the entire viral genome and acted as the basis for primer design. On the contrary, the longest contig we generated (29,802 nt) showed a nearly complete match with reference MN908947.3. Consequently, the published sequence data cannot be the original short reads used for contig generation. This is to be regarded as extremely problematic in the context of scientific publications, since in this way it is no longer possible to verify the published results. The possibility to verify published scientific hypotheses is the essence of living science.

Contrary to what was reported in [1], we may have found contigs with high coverage associated with (ribosomal) ribonucleic acids of human origin. Thus, it is possible that not all human-associated nucleic acids were eliminated in the construction of SARS- CoV-2. Further, no evidence of the presence of viral nucleic acids in the patient sample was provided and, consequently, there is a possibility that human or nonviral nucleic acid fragments were used to construct the claimed viral sequence MN908947.3 to a significant extent without detection. This possibility would have to be excluded by control experiments.

In all publications on the reference genomes analyzed in this study, the necessary evidence on the exact origin of the sequence fragments used for construction was also not provided and the necessary control experiments were not published.

We would like to mention here that control experiments may have already been performed many times without being noticed, showing the possibility of constructing SARS-CoV-2 genomes from non-infectious human samples. For example, whole genome sequencing from samples with a baseline Ct value greater than 35 is reported in [5] and [17]. This could be a refutation for the viral model for SARS-CoV-2.

The analysis of the nucleotide coverage distributions as well as the length distributions of the mappable sequence reads for the respective reference sequences leads to the hypothesis of a possible unintentional amplification of sequence reads not associated with SARS-CoV-2. Further, along with this, the possibility of accidental generation of sequences that were not present in the initial sample but were generated only by the amplification conditions, such as the primer sequences used and the cycles performed, must be considered. This possibility therefore requires the performance of appropriate control experiments.

In addition to attempting to replicate the assembly published in [1] with the published sequence reads, we considered a simple approach for analyzing the internal structure of large datasets of short sequence reads. With the sequence data at hand, we were able to compute consensus sequences for the reference genomes LC312715.1 (HIV) and NC_001653.2 (Hepatitis delta virus) with higher goodness than for those reference sequences we considered associated with coronaviruses. This was particularly true for bat-SL-CoVZC45 (GenBank: MG772933.1), which led to the origin hypothesis of SARS-CoV-2. Thus, we were able to substantiate our hypothesis that the claimed viral genome sequences are misinterpretations in the sense that they have been or are being constructed unnoticed from non-viral nucleic acid fragments. In particular, our results underscore the urgent need to perform appropriate control experiments. For each suspected pathogenic viral genome sequence, an obvious protocol would be to attempt assembly of the genome sequences from corresponding non-suspect samples using identical protocols.

We observed high R1 and R2 error rates in the reference genomes for measles, Ebola, or Marburg, where the nucleic acid fragments used for construction were propagated in Vero cells. It remains an open question so far whether this is due to the nucleic acid sources themselves, or to the amplification conditions used (e.g. primer sequences and cycle number) or sequencing protocols (e.g. the polymerases and reverse transcriptases used).

With regard to our results, in addition to publishing the final sequence data used, we always recommend publishing sequence data that resulted only from amplification with random hexamers and moderate cycle numbers to provide the most unbiased data possible for structural analysis.

Material and methods

Coverage depth of a reference sequence with short sequence reads

Let 𝐺 denote the length of the reference sequence, Ø𝐿 the average read length, 𝑛 the number of short sequences reads, and 𝑁 the random average depth of coverage of the reference sequence with the short sequence reads. Then

The expression ^Ø𝐿/G can be viewed as the probability of coverage of a nucleotide within the reference sequence with a short sequence read.

Generation of random reference sequences

The following theorem allows the simulation of a random variable 𝑋 with cumulative distribution function 𝐹.

Theorem (Inversion principle) [28].
Let 𝑈 be a random variable equally distributed on the interval (0,1). Let 𝑋 be a random variable with cumulative distribution function 𝐹, and let

𝐹⁻¹(𝑦) ≔ inf {𝑥 ∈ ℝ|𝐹(𝑥) ≥ 𝑦}.

Then applies

𝐹⁻¹(𝑈) ~ 𝑋.

Let 𝑈𝑖, 𝑖 = 1, … ,29.903 be independently identical equally distributed random variables on the interval (0,1). Let 𝑝_𝑛𝑡, 𝑛𝑡 ∈ {𝐴, 𝑇, 𝐶, 𝐺} denote the probability for the nucleotide 𝑛𝑡. Then the nucleotide 𝑁_𝑖, 𝑖 = 1, … ,29.903 of the randomly generated reference sequence is obtained via

For the reference sequence "rnd_unifom", the uniform distribution on the set {𝐴, 𝑇, 𝐶, 𝐺} was used. To simulate the random reference sequence "rnd_wuhan", the relative occurrence of nucleotides A, T, C and G in the genome sequence for SARS-CoV-2 (GenBank: MN908947.3) was chosen as the nucleotide distribution. In the construction of the randomized reference sequences "rnd_wh_mk_1" and "rnd_wh_mk_2", the conditional probability, conditional on the last and on the last two nucleotides, respectively, was chosen according to the corresponding empirical frequencies in the sequence for SARS-CoV-2 (GenBank: MN908947.3).

Stochastic simulation of random coverages of a reference sequence

The cumulative distribution function of the exponential distribution with parameter 𝜆 is [28],

 Let 𝑋 be a random variable with distribution function 𝐹. Then holds

Bioinformatics methods (structural analysis)

1. Mapping using BBMap

bbmap.sh ref=$reference.fasta

mapPacBio.sh in=SRR10971381_1.fastq in2=SRR10971381_2.fastq outm=mapped.sam vslow k=8 maxindel=0 minratio=0.1

2. Selection of the mapped sequences depending on M1 and M2 using BBMap (reformat.sh)

reformat.sh in=mapped.sam out=sample_selection.sam minlength=$M1 (maxlength=100) idfilter=$M2 ow=t

3. Calculation of the consensus sequence

3.1 Preparation using Samtools

samtools view -b sample_selection.sam > sample.bam samtools sort sample.bam -o sample_sort_reads.bam samtools index sample_sort_reads.bam

3.2 Determination of the preliminary consensus sequence

samtools mpileup -uf mapping/$reference.fasta sample_sort_reads.bam | bcftools call -c | vcfutils.pl vcf2fq > SAMPLE_cns.fastq

3.3 Determination of the final consensus sequence (min. Q20)

seqtk seq -aQ64 -q20 -n N sample_cns.fastq > sample_cns.fasta

4. Mapping of the consensus sequence to the reference sequence using BWA.

bwa index $reference.fasta

bwa mem $reference.fasta sample_cns.fasta > sample_cns.sam

5. Review with Tablet and Excel

The assessment was performed using Tablet software for visualization of sequence data and Excel spreadsheet program.

References

1. Fan Wu u. a. A new coronavirus associated with human respiratory disease in China. In: Nature 580.7803 (2020). DOI: 10.1038/s41586-020-2202-3.

2. Na Zhu u. a. A Novel Coronavirus from Patients with Pneumonia in China, 2019. In: New England Journal of Medicine 382.8 (2020), S. 727-733. DOI:10.1056/nejmoa2001017.

3. Divinlal Harilal u. a. SARS-CoV-2 Whole Genome Amplication and Sequencing for Effective Population-Based Surveillance and Control of Viral Transmission. In: Clinical Chemistry 66.11 (2020), S. 1450-1458. DOI: 10.1093/clinchem/hvaa187.

4. Jalees A. Nasir u. a. A Comparison of Whole Genome Sequencing of SARSCoV-2 Using Amplicon-Based Sequencing, Random Hexamers, and Bait Capture. In: Viruses 12.8 (2020), S. 895. DOI: 10.3390/v12080895.

5. Clinton R. Paden u. a. Rapid, sensitive, full-genome sequencing of severe acute respiratory syndrome coronavirus 2. In: Emerging Infectious Diseases 26.10 (2020), S. 2401-2405. DOI: 10.3201/eid2610.201800.

6. Sureshnee Pillay u. a. Whole Genome Sequencing of SARS-CoV-2: Adapting Illumina Protocols for Quick and Accurate Outbreak Investigation during a Pandemic. In: Genes 11.8 (2020), S. 949. DOI: 10.3390/genes11080949.

7. Dan Hu u. a. Genomic characterization and infectivity of a novel SARS-like coronavirus in Chinese bats. In: Emerging Microbes & Infections 7.1 (2018), S. 1-10. DOI: 10.1038/s41426-018-0155-5.

8. Davaalkham Jagdagsuren u. a. The second molecular epidemiological study of HIV infection in Mongolia between 2010 and 2016. In: Plos One 12.12 (2017). DOI: 10.1371/journal.pone.0189605.

9. J. A. Saldanha, H. C. Thomas und J. P. Monjardino. Cloning and sequencing of RNA of hepatitis delta virus isolated from human serum. In: Journal of General Virology 71.7 (1990), S. 1603-1606. DOI: 10.1099/0022-1317-71-7-1603.

10. Jernej Mlakar u. a. Zika Virus Associated with Microcephaly. In: New England Journal of Medicine 374.10 (2016), S. 951-958. DOI: 10.1056 /nejmoa1600651.

11. Christopher L. Parks u. a. Comparison of Predicted Amino Acid Sequences of Measles Virus Strains in the Edmonston Vaccine Lineage. In: Journal of Virology 75.2 (2001), S. 910-920. DOI: 10.1128/jvi.75.2.910-920.2001.

12. Konstantin M. J. Sparrer u. a. Complete Genome Sequence of a Wild-Type Measles Virus Isolated during the Spring 2013 Epidemic in Germany. In: Genome Announcements 2.2 (2014). DOI: 10.1128/genomea.00157-14.

13. Paul A. Rota u. a. Characterization of a Novel Coronavirus Associated with Severe Acute Respiratory Syndrome. In: Science 300.5624 (2003), S. 1394- 1399. DOI: 10.1126/science.1085952.

1. Runtao He u. a. Analysis of multimerization of the SARS coronavirus nucleocapsid protein. In: Biochemical and Biophysical Research Communications 316.2 (2004), S. 476-483. DOI: 10.1016/j.bbrc.2004.02.074.

2. Tracey Goldstein u. a. The discovery of Bombali virus adds further support for bats as hosts of ebolaviruses. In: Nature Microbiology 3.10 (2018), S. 1084- 1089. DOI: 10.1038/s41564-018-0227-2.

3. Jonathan S. Towner u. a. Marburgvirus Genomics and Association with a Large Hemorrhagic Fever Outbreak in Angola. In: Journal of Virology 80.13 (2006), S. 6497-6516. DOI: 10.1128/jvi.00069-06.

4. Annika Brinkmann u. a. Amplicov: Rapid whole-genome sequencing using multiplex PCR amplication and real-time Oxford Nanopore minion sequencing enables rapid variant identication of SARS-COV-2. In: Frontiers in Microbiology 12 (2021). DOI: 10.3389/fmicb.2021.651151.

5. SARS-COV-2. url: https://artic.network/ncov-2019.

6. Ncbi. ncbi/sra-tools: SRA Tools. URL: https://github.com/ncbi/sra-tools.

[20a] Dinghua Li u. a. MEGAHIT: an ultra-fast single-node solution for large and complex metagenomics assembly via succinct de Bruijn graph. In: Bioinformatics 31.10 (2015), S. 1674-1676. DOI: 10.1093/bioinformatics/btv033.

[20b] Voutcn. voutcn/megahit: Ultra-fast and memory-ecient (meta-)genome assembler. URL: https://github.com/voutcn/megahit.

[21a]  Shifu Chen u. a. fastp: an ultra-fast all-in-one FASTQ preprocessor. In:

Bioinformatics 34.17 (2018), S. i884-i890. DOI: 10.1093/bioinformatics/bty560.

[21b] OpenGene. OpenGene/fastp: An ultra-fast all-in-one FASTQ preprocessor (QC/adapters/trimming/ltering/splitting/merging...) URL: 

https://github

. com/OpenGene/fastp.

[22a] Ben Langmead u. a. Scaling read aligners to hundreds of threads on generalpurpose processors. In: Bioinformatics 35.3 (2018), S. 421-432. DOI:

10. 1093/bioinformatics/bty648.

[22b] Ben Langmead. BenLangmead/bowtie2: A fast and sensitive gapped read aligner. URL: https://github.com/BenLangmead/bowtie2.

[23a] Brian Bushnell. BBMap: A Fast, Accurate, Splice-Aware Aligner. In: (March 2014). URL: https://www.osti.gov/biblio/1241166.

[23b]  BBMap. url: https://sourceforge.net/projects/bbmap/.

[24a] Li H. Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. In: (May 2013). URL: https://arxiv.org/abs/1303.3997.

[24b] lh3. lh3/bwa: Burrow-Wheeler Aligner for short-read alignment (see mini-map2 for long-read alignment). URL: https://github.com/lh3/bwa.

[25a] H. Li u. a. The Sequence Alignment/Map format and SAMtools. In: Bioinformatics 25.16 (2009), S. 2078-2079. DOI: 10.1093/bioinformatics/btp352.

[25b]  Samtools. url: 

http://www.htslib.org/

[25c] P. Danecek u. a. Twelve years of SAMtools and BCFtools. In: GigaScience 10.2 (2021). DOI: 10.1093/gigascience/giab008.

[25d] P. Danecek u. a. The variant call format and VCFtools". In: Bioinformatics 27.15 (2011), S. 2156-2158. DOI: 10.1093/bioinformatics/btr330.

[26] Tablet. URL: https://ics.hutton.ac.uk/tablet/.

[27a] Wei Shen u. a. SeqKit: A Cross-Platform and Ultrafast Toolkit for FASTA/Q File Manipulation. In: Plos One 11.10 (2016). DOI: 10.1371/journal.pone.0163962.

[27b] lh3. lh3/seqtk: Toolkit for processing sequences in FASTA/Q formats. URL: https://github.com/lh3/seqtk.

[28] Albrecht Irle. Wahrscheinlichkeitstheorie und Statistik: Grundlagen - Resultate - Anwendungen. Teubner, 2010.